FFT란 무엇인가? 나도 모른다. 하지만 간략하게 뭔지 알아 볼 수는 있다.
대략 Fast Fourier Transform이라는 것의 약자이다. 빠른 푸리어 변환 이라는 의미다. 푸리에는 사람 이름이고, 옛날 물리학자다. 뉴튼같은 사람이라고 보면 된다.
그런데 왜 빠른(fast)를 사용하나? 나도 잘 모르지만, 음악에서는 거의 FFT를 쓰고, 간혹 Descrete인 DFT를 쓰는 분야도 있다고 한다. 거기까진 모르겠다.
그러면 Pd에서 해볼 수 있으니 한번 해보자. 뭔가 대단한 걸 하는 건 절대 아니고, 그냥 맛만 보는 것이다.
초보자를 위해 대략적인 개념은 이렇다.
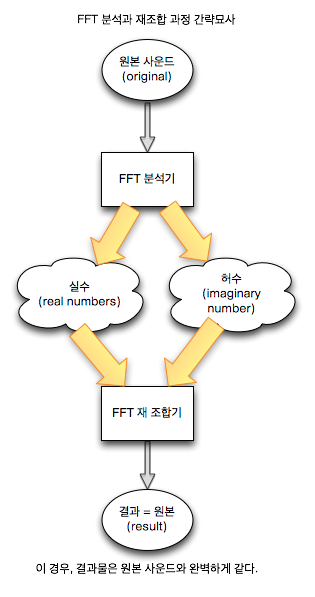
그러니까 원본 사운드를 넣어서 분석기로 분해한 다음에 다시 재 조합하면 원본과 같은 사운드가 나온다. 물론 FFT를 하는 목적은 분해한 다음에 뭔가를 해야 하지만, 우리는 초보자이기에 그냥 다시 합친다. 예를 들면 그냥 개구리 배를 갈랐다가, 다시 배를 꼬맨 다음에, 개구리가 살아나게 하는 것 같은 거다. 개구리가 죽으면 실패고, 살아나면 성공이다. 그럼 개구리를 살려보자.
중요한 것은 FFT를 거치면 실수부와 허수부로 나뉜다는 것이다. 실수와 허수에 대해서는 수학의 정석을 찾아보라. 나는 모른다.
실수부는 real part라고 하며, 허수부는 imaginary part라고 한다. 고도의 뛰어난 이펙터들은 이 분해된 실수부와 허수부를 재 조합하여 아름다운 소리를 만들어 낸다. 그것은 나중에 고수가 되면 해보자.
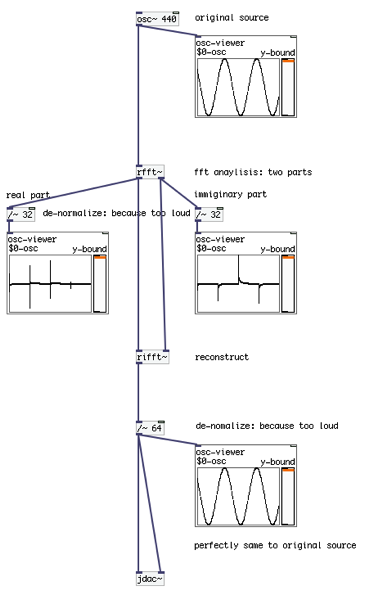
일단 Pd에서 위에서 설명한 개구리 배 갈랐다 다시 꼬매서 살아나게 하는 것을 해보자. 패치는 다음과 같다.
각 파트마다 오실레이터(Oscilator)를 달아 놔서 파형을 확인해 볼 수 있게 해 놓았다. 마지막에 /~64로 나누는 이유는 재 조합된 소리가 너무 커서 다시 줄이는(de-normalize) 것이다. 이와 같이 FFT의 원리에 대해 대충 맛만 보았다. 다음에는 좀 더 공부해서 쓸만한 것을 공유해 보겠다.
패치를 만들어 보실 분들을 위해 다시 적어보겠다. 형식은 웹에서 사용하는 형식이다. 익숙해 지면 편하다.
[osc~ 440] <<= 임의의 소리, 아무거나 해도 된다.
|
[rfft~]
| \
[rifft~]
|
[/~ 64]
|
[dac~] <<= 기회는 평등할 것입니다. 과정은 공정할 것입니다. 결과물은 원본과 같을 것 입니다…!
이해는 안되겠지만, 그냥 맛만 보는데 의의를 두자.
Pd Patch를 첨부한다.
https://docs.google.com/file/d/0B42bn7ncw918dm9PVUZnNUtyRGc/edit?usp=docslist_api
끝
No comments:
Post a Comment