Pd에서 2차 함수 곡선 사용하기

0에서 1까지 슬라이더를 만들었다. 그런데 항상 1:1로 증가하면 재미가 없다. 그래서 처음에는 완만하게 증가하다 나중에 많이 증가하는 함수를 만들어 보자.

보통 당연히 0부터 1까지 증가하면 정비례로 증가하게 된다. 이런 식이다 편의상 1부터 5까지 하겠다.

정비례 증가
1 2 3 4 5
1 2 3 4 5

정비례 증가를 Pd에서 나타내 보겠다. 너무 당연해서 시시하다. 두 개의 슬라이더는 링크되어 당연히 똑같이 움직일 것이다.


하지만 이렇게 하고 싶다면? 예제가 대충 무슨 말인지 알 것이다. 1부터 5로 증가하는데, 결과는 차츰 증가하다가 나중에 많이 커진다.
1      2        3       4      5
1      1.1    1.5    3       5

그래프로 그려 보자면 이렇다.


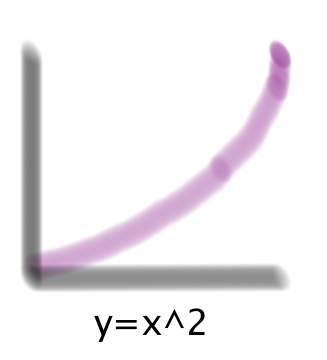
x는 순차적으로 커지는데, y는 조금씩 커지다가 나중에 더 많이 커진다. 이것을 Pd에서 나타내 보면 이렇다.


[expr] 을 쓰고 있다. expression이라는 것의 줄임말이다. 이것은 수학 공식을 쉽게 쓰기 위한 객체이다.
$f1 은 들어온 값을 말한다. 그리고 *는 곱하기다.  그러므로 들어온 값을 서로 곱하면 된다.
이것이 x^2 (엑스 제곱)을 표현하는 식이다.

그러면 이런 것도 가능할까? y 값이 처음에 많이 커지다가 나중에 조금씩 커지는 모양이다. 이것도 2차 함수이긴 하지만 표현식이 조금 다르다.


Pd에서 나타내면 약간 이상한 모양이 나오지만 수학적으로는 이렇게 하면 된다. 나도 수학 전공은 아니라 모르겠지만 아무튼 나는 이렇게 한다.

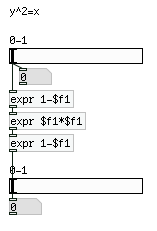
이것을 하려고 수학의 정석 책을 뒤져가면서 했는데, 지금은 어떻게 했는지 까먹어서 간략하게 설명하겠다.
처음 값은 0에서 1까지다. 편의상 0 to 1 이라고 하겠다.
[expr 1-$f1] 은 들어온 값을 1 to 0으로 돌려 주는 것이다.
[expr $f1*$f1] 은 y=x^2과 같이 작동하는데 값이 반대로 되어 있다.
[expr 1-$f1]은 1 to 0 을 다시 0 to 1 으로 바꿔 주는 것이다.

동작 영상을 한번 봅시다.
http://youtu.be/JIfQjZOhgVw


물론 2차 함수 곡선 이외에도, [expr $f1*$f1*$f1] 으로 하면 3차 곡선이고 4번 하면 4차 곡선이다.

끝